Analyze 3D atomistic models

Atomes offers to compute a number of physico-chemical properties for any 3D atomistic models (see the list bellow).

Calculation results are handled within the software using a comprehensive graph edition system:

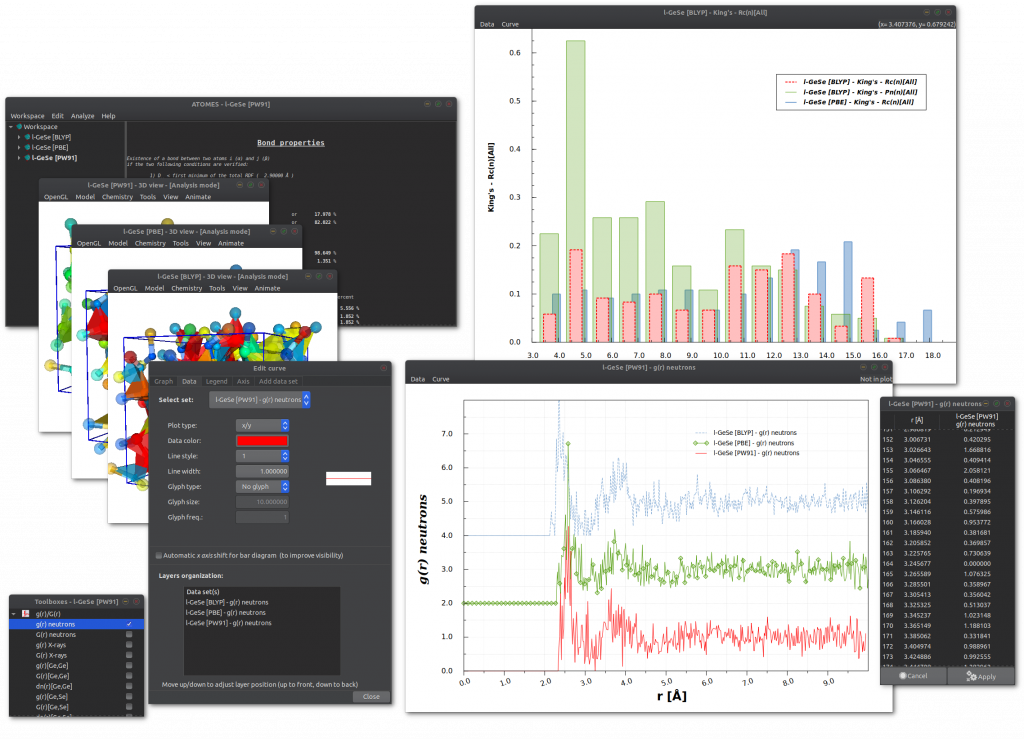
Atomes regroups the following physico-chemical analyses:

• Radial distribution functions g(r) (RDFs) [1] including:
  • Total RDFs for neutrons and X-rays.
  • Partial RDFs.
  • Bhatia-Thornton RDFs [2]
  • Radial distribution functions can be computed by:
    • direct real space calculation
    • Fourier transforming of the structure factor calculated using the Debye formalism [3]
• Structure factors S(q) [3] including:
  • Total structure factors S(q) for neutrons and X-rays.
  • Total Q(q) [3], [4] for neutrons and X-rays.
  • Partial S(q):
    • Faber-Ziman [5] partial S(q)
    • Ashcroft-Langreth [6], [7], [8] partial S(q)
    • Bhatia-Thornton [9] partial S(q)
  • Structure factors can be computed by:
    • Fourier transforming of the radial distribution functions
    • using the Debye formalism [3]
• Interatomic bond properties
  • Coordination numbers
  • Atomic near neighbor distribution
  • Fraction of tetrahedral units
  • Bond length distribution for the first coordination sphere
• Distribution of bond angles
• Distribution of dihedral angles
• Ring statistics, according to several definitions:
  • All closed paths (no rules)
  • King’s rings [10], [11]
  • Guttman’s rings [12]
  • Primitive rings [13], [14] (or Irreducible [15])
  • Strong rings [13], [14]
  • And including options to:
    • search only for ABAB rings
    • exclude rings with homopolar bonds (A-A or B-B) from the analysis
• Chain statistics, including options to:
  • search only for AAAA chains
  • search only for ABAB chains
  • exclude chains with homopolar bonds (A-A or B-B) from the analysis
  • search only for 1-(2)_n-1 chains
• Spherical harmonics invariant, Q_l, as local atomic ordering symmetry identifiers [7]
  • Average Q_l for each chemical species
  • Average Q_l for a user specified structural unit
• Mean Square Displacement of atoms (MSD)
  • Atomic species MSD
  • Directional MSD (x, y, z, xy, xz, yz)
  • Drift of the center of mass

See appendix 5 of the documentation to learn more about the physics and the chemistry behind these calculations.

For more about running calculation using atomes see documentation chapter 4.

References

1. M. P. Allen and D. J. Tildesley, Computer simulation of liquids. Oxford science publications, 1987.
2. P. S. Salmon, J. Non-Cryst. Solids, vol. 353, pp. 2959–2974, 2007.
3. M. T. Dove, M. G. Tucker, and D. A. Keen, Eur. Jour. Mat., vol. 14, pp. 331–348, 2002.
4. B. Thijsse, J. App. Cryst., vol. 17, pp. 61–76, 1984.
5. T. E. Faber and Z. J. M., Phil. Mag., vol. 11, no. 109, pp. 153–173, 1965.
6. N. W. Ashcroft and D. C. Langreth, Phys. Rev., vol. 156, no. 3, pp. 685–692, 1967.
7. N. W. Ashcroft and D. C. Langreth, Phys. Rev., vol. 159, no. 3, pp. 500–510, 1967.
8. N. W. Ashcroft and D. C. Langreth, Phys. Rev., vol. 166, no. 3, p. 934, 1968.
9. A. B. Bhatia and D. E. Thornton, Phys. Rev. B., vol. 2, no. 8, pp. 3004–3012, 1970.
10. S. V. King, Nat., vol. 213, p. 1112, 1967.
11. D. S. Franzblau, Phys. Rev. B., vol. 44, no. 10, pp. 4925–4930, 1991.
12. L. Guttman, J. Non-Cryst. Solids, vol. 116, pp. 145–147, 1990.
13. K. Goetzke and H. J. Klein, J. Non-Cryst. Solids, vol. 127, pp. 215–220, 1991.
14. X. Yuan and A. N. Cormack, Comp. Mat. Sci., vol. 24, pp. 343–360, 2002.
15. F. Wooten, Act. Cryst. A, vol. 58, no. 4, pp. 346–351, 2002.
16. S. Le Roux and P. Jund, Comp. Mat. Sci., vol. 49, pp. 70–83, 2010.
17. P. Steinhardt, D. R. Nelson, and M. Ronchetti, Phys. Rev. B., vol. 28, no. 2, pp. 784–805, 1983